Having the ability to predict the thermal behavior of discrete semiconductor devices and their packaging can be critical for some applications and can be done using Foster and Cauer RC models. In this blog, Nexperia reviews the theory behind them, discusses their benefits and limitations for determining the temperature of a device, and shows where designers can access them for many of discrete devices, including its range of bipolar junction transistors (BJT).
Use thermal resistance to calculate device temperature rise
The thermal impedance (Zth) of a semiconductor device can be determined by measuring the power losses that occur when applying step voltages of varying time intervals to it. A device subjected to a power pulse for more than one second (approximately) is considered to be in a steady-state and therefore in thermal equilibrium. Here, Zth reaches a plateau and this value is then referred to as thermal resistance (Rth). Thermal resistance curves Rth(j−sp) from the device junction-to-solder point for the PBSS4310PAS-Q DFN2020D-3 low-VCEsat BJT with pulses of different duty cycles are shown in Figure 1. These curves represent additional temperature rise due to RMS power dissipation. To calculate the temperature rise in the junction of a device with a single active area (i.e., a heat source at the junction), the power and duration of the pulse applied to the device must be known. If this has a square shape, then the thermal impedance can be read directly from the Zth chart and then multiplying this value by the power gives the temperature rise within the junction.
However, for a transient pulse, e.g., sinusoidal or pulsed, the temperature rise in the device junction is more difficult to calculate. To calculate Zth as a function of time, a device is instead thermally modeled as an RC ladder. This thermal model for Zth (which is analogous to an electrical model) can then be used in a SPICE simulation environment to calculate junction temperature. The thermal-electrical analogy is summarized in Table 1.

Foster and Cauer RC models
The Foster model
A Foster model is derived by semi-empirically fitting a curve to Zth, resulting in the one-dimensional RC network shown in Figure 2. It is important to note that the R and C values in a Foster model do not correlate with actual locations on a physical device meaning they can’t be calculated from device material constants as is the case in other thermal models. Furthermore, a Foster RC model cannot be subdivided or interconnected e.g. it can’t be used alongside the model for a heatsink or other external components.

By measuring heating (or cooling) and generating a Zth curve for a device, Equation 2 can then be used to generate a fitted curve like that shown in Figure 3.
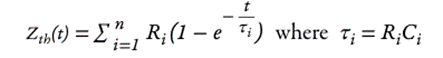
The model parameters Ri and Ci are the thermal resistance and capacitance values used to create the thermal model.

The Cauer model
A Cauer model is also represented by RC network, but unlike the Foster model, thermal capacitances are connected to thermal ground (ambient temperature location) as shown in Figure 4, and they also have physical meaning, which allows them to be used in determining the temperature of internal layers within a semiconductor structure. An advantage of using the Cauer model is that it allows the addition of external components to the device model, for example, the thermal models for PCBs, heatsinks, etc.

Limitations of thermal models
Foster and Cauer RC thermal models allow application engineers to quickly perform calculations of the transient response of a device package to complex power profiles, but they are not perfect. The physical materials used to build semiconductors have temperature-dependent characteristics. These mean that thermal resistance is a temperature-dependent parameter, whereas with Ohm’s law, ohmic resistance is typically considered to be constant i.e. independent of voltage. As a result, electrical and thermal parameters are not exactly equivalent, but provide a solid basis for fundamental thermal simulations. A further limitation of thermal models is that the mounting base temperature of a device Tmb is assumed to be isothermal (has a constant temperature). This is rarely the case in practice, in which case the rise in temperature of the mounting base must also be factored into calculations. This is determined by calculating the temperature rise due to the average power dissipation (i.e., the heat flow) from the mounting base through to ambient temperature location. Consequently, these models are of limited use for pulses greater than 1s, after which time heat begins to flow into the external environment of the device. In this scenario, the thermal models for external devices like the PCB, heatsink and other materials in the proximity of the semiconductor component must be also included.
Nexperia offers Foster and Cauer models to simplify thermal design
Nexperia provides Foster and Cauer RC thermal models for many of its discrete devices including BJTs, diodes and power MOSFETs. These models, which can be accessed within individual product pages on Nexperia’s website, are compatible with SPICE and other simulation tools and can be used to simulate the junction temperature rise in transient conditions. They provide a simple and accurate method for application engineers to quickly perform a thermal design.
To learn more about how to use Foster and Cauer device models in your thermal design, visit Nexperia’s BJT application handbook at: